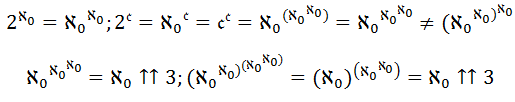Kevin's Watch

The Stanford Encyclopedia of Philosophy has a great intro/overview of the subject. I'd also recommend Conway and Guy's The Book of Numbers since it shows how Cantor came up with the expression "2 to the power of aleph-zero" in the first place (it wasn't originally the powerset operation as fully codified in set theory; I mean it technically was, but he didn't explain it as such until later, I believe).

So without further adieu [I've sent this to some professors and uploaded it to a forum I'm also a member of, The 17th Shard]. Keep in mind, there are a few typos that I marked off on The 17th Shard, but I don't have time to dwell on them right now haha.

















That's not all there is to it, but I am outta time for now

+JMJ+

Mig's back!

Woot!

and in style

Mighara, I'm sorry, but I am kind of at the level of, "I am clear on ways we could create a mapping from the integers to the rationals, so they're the same cardinality."
And... "I know the reals are a higher cardinality than the integers, and that's reasonable and there's a proof."

But, nonetheless, could you post more?

Hashi, if you help me (and maybe a few other people not on the Watch!) learn pre-requisites pick through Mig's attempt to prove this, I will literally...

...hold your beer.

I figured that aleph-zero to the power of the Continuum equals the Continuum to the power of the Continuum, as 2 to the power of the Continuum equals the Continuum to the power of the Continuum, and you can switch out aleph-zero for 2 in these kinds of cases. Now the Continuum to the power of aleph-zero is the Continuum, interestingly enough, though aleph-omega to the power of aleph-zero is greater than aleph-omega. Something changes at aleph-omega, then, and I think this has to do with the way the "staircases" work at this point. (There was a simple proof of this I found having to do with the epsilon numbers, IIRC, but I don't recall what it was right now.)

No one usually uses Knuth-arrow tetration notation in this context. I mean I've seen it done, like omega tetrated by omega equals epsilon-zero (this I saw on the Mathematics Stack Exchange). To get a feel for the tetration notation here: take 2^2^2 or 3^3^3^3. These are simplified in the Knuth notation as 2 ↑↑ 3 and 3 ↑↑ 4. So aleph-zero to the power of aleph-zero can be reset to aleph-zero ↑↑ 2, and the Continuum to the power of the Continuum can be reset to c ↑↑ 2. Now since c equals aleph-zero^aleph-zero, it follows that you can put aleph-zero^aleph-zero in parentheses and switch that out for c wherever you start out with c. So aleph-zero to the power of the Continuum can be rewritten as aleph-zero^(aleph-zero^aleph-zero). Now if the parentheses surrounded the first two aleph-zero marks, you wouldn't be able to rewrite the total as aleph-zero ↑↑ 3, but otherwise then aleph-zero^(aleph-zero^aleph-zero) can be rewritten as aleph-zero ↑↑ 3.

OTOH, (aleph-zero^aleph-zero)^(aleph-zero^aleph-zero) wouldn't be rewritten as aleph-zero ↑↑ 4 because you'd have to evaluate within the parentheses first (PEMDAS, even at this level).* This is all subtle enough that it took me months of artificially induced stress to even start to notice what goes on in this case,** so I suppose that it would be even easier to miss if you never tended to focus on the "aleph-zero ↑↑ 2" formulation and stuck with the classical "2 to the power of aleph-zero."

*This might seem obviously false. However, the requirements that you be able to replace c with aleph-zero in the base case, and either of these with 2, and that you would evaluate the staircase in descending order if no parentheses were used (this is an independent rule for evaluating power-towers in general: see https://mathvault.ca/derivative-tetrati ... entiation/), both combine to make the proposition less-than-obviously, but still provably, true.

**I deliberately blew off a lot of normal social "responsibilities" in order to stress myself out enough to believe, "If I don't solve this problem, I'm screwed," and voila, I solved the problem the wrong way the first time around: I spent a month and a half trying to show the c equals aleph-(omega.1) and it was almost purely by accident that I realized my mistake.

EDIT:



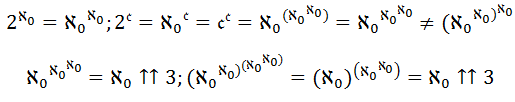
EDIT 2: I found out you can check some of my claims directly using https://www.wolframalpha.com/ I.e. if you put in "aleph 0 ^ aleph 0 ^ aleph 0" you get aleph-2 (with the caveat that this computation presupposes the Generalized Continuum Hypothesis) and you also get aleph-2 if you input "(aleph 0 ^ aleph 0) ^ (aleph 0 ^ aleph 0)." So the parenthetical four-place argument is equivalent to the three-place one with no parentheses. Also, instead of c, they use beth-1 for the Continuum, so you can check that "c^c" = "aleph 0 ^ aleph 0 ^ aleph 0" with reference to the beth-arithmetic (input "beth 1 ^ beth 1").